چرخ دنده

مقدمه

احتمالا کلمه ی “چرخ دنده” به گوش تان خورده است. چرخ دنده ها کاربرد فراوانی در زندگی روزمره ما دارند چرا که امروزه، ماشین ها عضو های جدایی ناپذیر زندگی انسان شده اند و چرخ دنده ها نیز یکی از اصلی ترین اجزای اصلی ماشین ها هستند. همان طور که از اسم آن مشخص است، چرخ دنده ها چرخ ها یا دیسک های دندانه داری هستند که بر روی هم سوار می شوند یا اصطلاحا “درگیر” می شوند. از این طریق، سرعت و گشتاور را به چرخ دنده و محور دیگر منتقل می کنند. به عبارت دیگر وظیفه اصلی چرخ دنده ها انتقال حرکت و قدرت از یک محور دوار به محور دیگر می باشد. از این رو، در صنعت کاربرد فراوانی دارند. و اما سوال اصلی این است که اساس کار چرخ دنده ها چیست و اجزاء اصلی آنها چه هستند؟ دقیقا چگونه سرعت و گشتاور را منتقل می کنند؟ سیستم های چرخ دنده ای کجا کاربرد دارند؟ در این مقاله به تمامی این پرسش ها پاسخ خواهد داده شد.

اساس کار چرخ دنده ها و معرفی اجزاء آن ها

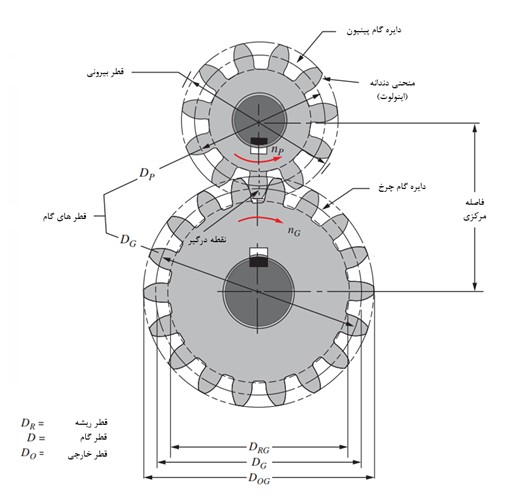
در یک مکانیزم ساده چرخ دنده ای، که دو چرخ دنده با هم درگیر شده باشند، برحسب قرارداد چرخ دنده ی کوچک را پینیون  (pinion) و چرخ دنده بزرگ را چرخ یا همان چرخ دنده (gear) می نامند. یا در ادبیاتی دیگر، چرخ دنده ها را تحت عنوان”راننده” یا (driver) – که معمولا به موتور وصل می شود و ورودی می باشد  – یا “رونده” یا (driven) – چرخ دنده ای که توسط چرخ دنده راننده یا ورودی رانده می شود – می نامند. اصلی ترین ویژگی مکانیزم های چرخ دنده ای تولید “مزیت مکانیکی” است. بدین معنا که طبق شکل زیر، اگر چرخ دنده با گشتاور  و سرعت زاویه ای  چرخ دنده ی پینیون را با گشتاور   و سرعت زاویه ای  را به حرکت دراورد، نیروی F مماس بر دایره های گام چرخ دنده ها به صورت مشترک که ناشی از تماس و درگیری دندانه ها می باشد، پدیدار می شود. دایره ی گام، دایره ای فرضی است که نقطه ی تماس دندانه ها روی آن می باشد و در ادامه معرفی خواهد شد.

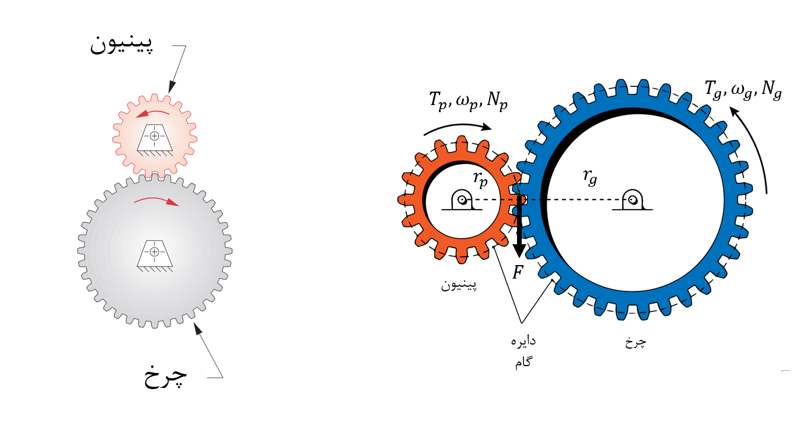
در سیستم چرخ دنده ای نشان داده شده، نیروی F برای هردو چرخ دنده ثابت است ولی گشتاور این نیرو برای دو چرخ دنده ثابت نیست چرا که بازوی گشتاور این نیرو که همان شعاع دایره گام می باشد برای دو چرخ دنده متفاوت است. لذا. بدیهی است که چرخ دنده پینیون گشتاور کمتری دارد چرا که شعاع آن طبق شکل کمتر است. بنابراین مزیت مکانیکی سیستم چرخ دنده ای زیر را تعریف میکنیم:

لازم به ذکر است که  نسبت شعاع ها با نسبت تعداد دندانه ها متناسب است و با نسبت سرعت های زاویه ای نسبت عکس دارد. و اما چرا؟  گفتیم که نقطه ی تماس دو چرخ دنده بر روی دایره ی گام آن ها صورت می گیرد. لذا حرکت دورانی این دو دایره به هم در نطقه ی تماسشون وابسته می باشد، پس اگر شعاع دایره پینیون را نصف شعاع دایره چرخ دنده بزرگتر در نظر بگیریم، با یک دور دوران چرخ دنده بزرگ و دو دور دوران پینیون نقاط مشترک متناظر چرخ دنده ها به هم می رسند. لذا سرعت دوران پینیون دو برار سرعت چرخ بزرگ است. درحالی که گشتاور آن نصف بود. پس نتیجه گیری می شود که نسبت گشتاور و سرعت زاویه چرخ دنده ها عکس هم می باشد.  برقراری رابطه بالا را به “قضیه اساسی چرخ دنده ها” نیز می شناسند که بیان می کند” نسبت سرعت های زاویه ای چرخ دنده هایی که با هم درگیر هستند باید در طول درگیری عددی ثابت باشد.“ اگر هندسه و ساختار پروفیل دندانه های چرخ دنده ها دارای خطا باشد معمولا فرایند درگیری چرخ دنده ها در حین حرکت دارای ارتعاش بوده و به ازای سرعت ثابت چرخ دنده ورودی، سرعت خروجی متغیری مشاهده خواهد شد.

یکی از کاربرد های اصلی چرخ دنده ها کاهش سرعت و افزایش گشتاور می باشد که در اکثر دستگاه های صنعتی مورد استفاده قرار می گیرد. به این سیستم های چرخ دنده ای، اصطلاحا “مکانیزم انتقال قدرت کاهنده یا گیربکس های کاهنده“ نیز گفته می شود که در آن مزیت مکانیکی سیستم عددی بالاتر از 1 می باشد. بنابراین به عنوان یک قاعده کلی در نظر داریم که در حالت ایده آل – که اصل قضیه چرخ دنده ها برقرار باشد:

• اگر سرعت خروجی کاهش یابد، گشتاور خروجی به همان نسبت افزایش می یابد.
• اگر سرعت خروجی افزایش یابد، گشتاور خروجی به همان نسبت کاهش می یابد.

یکی دیگر از ویژگی های سیستم های چرخ دنده ای، معکوس کردن جهت دوران محور ها می باشد. به طوری که اگر یک شفت به صورت ساعتگرد دوران کند، با انتقال حرکت توسط چرخ دنده، جهت دوران شفت دیگر پادساعتگرد می شود. برای نگه داشتن جهت دوران از چرخ دنده واسط به نام idler استفاده می کنند که مطابق  شکل زیر می تواند قرار بگیرد.         

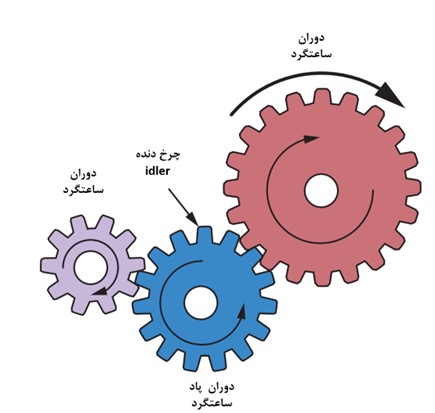
همانطور که پیش تر مطرح شد، شکل و هندسه پروفیل دندانه های چرخ دنده ها از اهمیت بالایی برخورد دار هستند چه که راندمان مکانیکی سیستم را تعیین می کنند. از این جهت به هندسه ی دندانه ها می پردازیم. اما ابتدا نیاز هست که درباره اجزای اصلی هندسی چرخ دنده ها توضیح داده شود.

مشخصات چرخ دنده ها

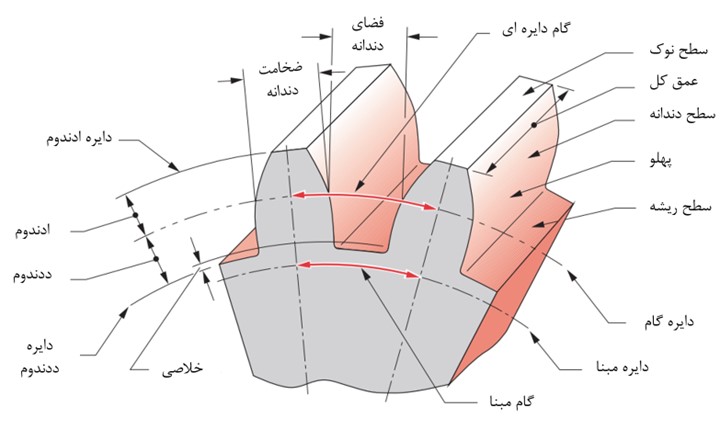
از مهم ترین مشخصات هندسی دندانه ها می توان به تعاریف زیر اشاره کرد.

دایره گام: Pitch Circle : وقتی دو چرخ دنده درگیر هستند، رفتار آن ها مانند رفتار دوغلتک که روی هم میغلتند مطابق شکل زیر می باشد. سطح این غلتک ها مشخص کننده دایره ای است که به آن دایره گام و به قطر آن، قطر گام می گویند. به عبارت دیگر، دایره های گام دو چرخ دنده درگیر با یکدیگر مماس و درگیر هستند و در حالت ایده آل بدون لغزش روی هم می غلتند. اگر اصطکاک کافی بین سطوح تماس وجود داشته باشد، انتقال نیرو و حرکت به خوبی صورت خواهد گرفت.

 قطر گام به عنوان یک پارامتر تئوریک (که در واقعیت قابل اندازه گیری نمی باشد) تعریف می شود که از مشخصه اصلی چرخ دنده های درگیر برای محاسبه سرعت زاویه ای های جفت چرخ دنده های درگیر استفاده می شود

گام دایره ای: Circular Pitch طول کمانی است بر روی قوس دایره گام بین منحنی های مربوط به دندانه های پهلوی هم که از رابطه زیر بدست می آید. (برحسب اینچ یا میلیمتر می باشد)

            که D قطر دایره گام و N تعداد دندانه ها هستند

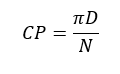
گام قطری : (diametral pitch) راه دیگری برای تعریف سایز دندانه تعریف آن بر قطر دایره گام است ( و نه روی محیط آن) که فقط بر حسب معکوس اینچ (1/inch) می باشد و در سیستم اندازه گذاری آمریکایی یا سیستم اینچی استفاده می شود.

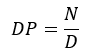
مدول: (module) عکس گام قطری تعریف می شود که در سیستم اندازه گذاری متریک استفاده می شود.

لازم به ذکر است که هردو چرخ دنده درگیر، باید گام قطری و یا مدول یکسانی داشته باشند.

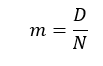
قطر ریشه دندانه (root diameter) : قطر دایره ای به مرکز چرخ دنده و شعاع واقع در ریشه ی دندانه که به آن دایره ددندوم نیز گفته می شود.

دایره خارجی (Outside diameter) : قطر دایره ای به مرکز چرخ دنده و شعاع واقع در نوک دندانه که به آن دایره ادندوم نیز گفته می شود.

قطر دایره مبنا(base circle) : قطر دایره ای به مرکز چرخ دنده و شعل واقع در فاصله ی لقی(clearance)  با شعاع دایره ددندوم که از رابطه زیر محاسبه می شود.

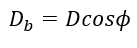
که  زاویه فشار می باشد که جلو تر معرفی می شود.

ادندوم (a): فاصله بین سر دندانه از دایره گام می باشد

ددندوم (d) : فاصله بین دایره گام و ریشه ی دندانه می باشد

عمق کل (ht): جمع ادندوم و ددندوم دندانه

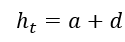
فاصله مرکزی (C): یکی از مهم ترین پارامتر های چرخ دنده ها فاصله خطی مرکز های آن ها می باشد که برابر با جمع شعاع های دایره های گام دو چرخ دنده در حالت ایده آل می باشد:

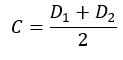
منحنی استاندارد دندانه ها

چرخ دنده ها دارای دندانه هایی هستند که با هم جفت می شوند و فرایند انتقال قدرت را پیش میبرند. از آنجا که سطح تماس دندانه ها و به دنباله آن هندسه ی سطح تماس نقش اساسی در روند انتقال گشتاور را ایفا می کند در این بخش به هندسه پروفیل استاندارد در چرخ دنده ها می پردازیم. یکی از متداول ترین پروفیل دندانه ها تحت عنوان “منحنی اینولوت” یا  involute curve می باشد که در اکثر صنایع دنیا کاربرد دارد. اصلی ترین ویژگی منحنی اینولوت برقراری نسبت سرعت زاویه ای ثابت بین دو چرخ دنده درگیر است (حتی اگر خطا در نصب محور های چرخ دنده در فاصله های تئوریک و لقی بین دندانه ها وجود داشته باشد). از لحظه ی اول درگیری و تماس دو دندانه، سرعت دورانی چرخ دنده اول با دوم متناسب است. در نتیجه، حرکت دورانی حاصل از این درگیری به صورت یکنواخت و روان صورت می گیرد. اگر عکس این اتفاق صورت بگیرد، شتاب های دورانی خصوصا در توقف و شروع حرکت پدیدار می شوند که به ارتعاش و نویز و از همه مهم تر لرزش دورانی که پدیده ای خطرناک می تواند باشد می انجامد.  شکل دندانه های با منحنی اینولوت را در شکل پایین مشاهده می کنید.

هندسه منحنی اینولوت:

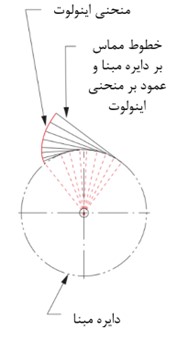
تصور کنید یک نخ را دور یک استوانه پیچیده اید. سپس نخ را به حالت سفت و کشیده در می آورید و آن را از بدنه استوانه به طوریکه نخ همواره بر دایره مماس باشد باز می کنید، انتهای نخ هنگام باز شدن منحنی اینولوت را مطابق شکل زیر تشکیل می دهد.

توجه داشته باشید که مرکز انحنای محنی اینولوت همواره بر روی سطح تماس نخ و استوانه می باشد. همچنین هر خطی که مماس بر منحنی اینولوت باشد، عمود بر نخ می باشد (همانند شکل زیر). بر همین اساس میتوان منحنی های اینولوت را برای چرخ دنده ها ترسیم کرد.

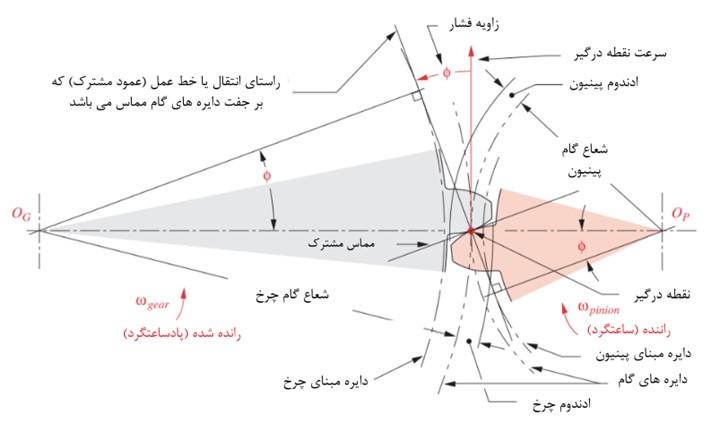
لازم به ذکر است که انحنای منحنی اینولوت دندانه ها با اندازه دایره پایه رابطه دارد به طوری که، با زیاد شدن شعاع دایره پایه، انحنای منحنی اینولوت را کم می کند و بالعاکس. یا به عبارتی : با زیاد شدن تعداد دندانه ها برای یک چرخ دنده با گام قطری مشخص، شعاع انحنای منحنی اینولوت دندانه ها افزایش می یابد که در شکل زیر مشاهده می کنید.

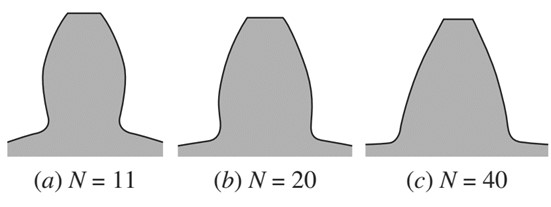
هندسه تماس بین دو چرخ دنده با دندانه های اینولوت:

همانطور که در شکل زیر نشان داده شده است، در نقطه تماس دو دندانه یا pitch point می توان دو خط ترسیم کرد که یکی مماس بر جفت سطوح تماس که مماس مشترک نامیده می شود و یکی دیگر که عمود بر مماس مشترک می باشد که عمود مشترک (یا محور انتقال) نامیده می شود در نظر گرفت. محور انتقال همواره از نقطه تماس دو دندانه  pitch pointعبور می کند. اگر نقطه آغاز درگیری و پایان درگیری جفت دندانه مجاور با محنی اینولوت را در نظر بگیریم، مشاهده می شود که محور های انتقال جفت دندانه ها از یک نقطه عبور می کند که این امر همان ویژگی اصلی منحنی اینولوت برای دندانه ها را به دنبال دارد.. زیرا این خاصیت باعث می شود نسبت سرعت ها ثابت بماند. لذا از این رفتار در درگیری دندانه های اینولوت نتیجه گیری می شود که: در تمام لحظات درگیری دندانه های اینولوت و انتقال قدرت از چرخ دنده ورودی به چرخ دنده خروجی، عمود مشترک ها یا محور های انتقال همواره باید از یک نقطه ی ثابت تماسی به نام pitch point بگذرد. خط عمل line of action، خط همان راستای مماس مشترک می باشد (مطابق شکل) است و به فاصله بین نقطه ی ابتدایی و انتهایی درگیری بر روی خط عمل، طول عمل یا Length of Action گفته می شود. درواقع نقطه درگیر دو دندانه در حین درگیری، از روی این خط عبور می کند.

زاویه فشار

 زاویه فشار زاویه بین خط مماس بر دایره گام که همان سرعت نقطه درگیر pitch می باشد و محور انتقال دندانه می باشد که یکی از متغیر های مهم هندسی دندانه ها هستند. اصولا، زاویه فشار اندازه قطر دایره مبنا  base diameterرا تعیین می کند و در نتیجه منحنی دندانه های اینولوت را نیز مشخص می کنند. در شکل زیر دندانه های اینولوت مختلف با زوایای فشار مختلف نشان داده شده اند.

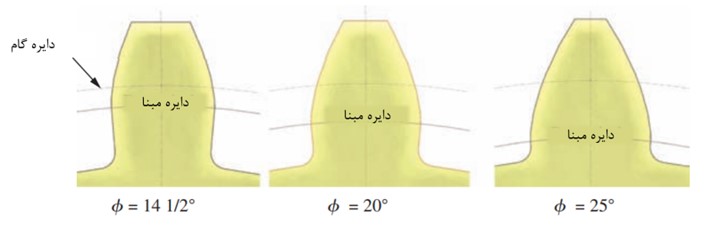
سازندگان چرخ دنده ها مقادیر استانداردی برای زاویه فشار اعلام کرده اند که از متداول ترین آن ها زوایای 14.5، 20، 25 درجه هستند. زاویه 20 درجه از مقادیر دیگر کاربرد بیشتر و زاویه 14.5 درجه کاربرد کمتری دارد. اگرچه طراحی و ساخت چرخ دنده هایی با زویای فشار متفاوت امکان پذیر است، اما توجیه اقتصادی آن نیز باید در نظر گرفته شود چرا که انتخاب زوایای فشار مختلف باعث ایجاد دندانه های اینولوت متفاوت می شود و فرایند ساخت و تراشیدن دندانه هارا ممکن است با چالش روبرو کند.

تغییر فاصله محور های چرخ دنده ها

گفته شد که فاصله ی محور های دو چرخ دنده در حالت ایده آل برابر است با جمع شعاع های دایره های گام آن ها. اما باید در نظر داشت که دایره گامی که چرخ دنده ها طبق آن ساخته می شوند همیشه ایده آل نیستن. درواقعیت مونتاژ چرخ دنده ها روی شفت هارا نمی توان به گونه ای انجام داد که فاصله شعاعی دو محور دقیقا منطبق با اندازه اسمی یا نامی آن ها باشد. . همچنین خطای های ساخت باعث ایجاد اختلاف بین فاصله شعاع های گام نامی و واقعی می شوند. اما لازم به ذکر است که مجموعه های چرخ دنده های درگیر می توانند در یک بازه ای محدود از فاصله مرکزی با هم درگیر شوند و اختلالی در روند کارکرد آن ها صورت نگیرد. اما چگونه می توان این خطا را جبران نمود ؟ به عنوان یک قاعده کلی داریم :

اگر دندانه های چرخ دنده های درگیر اینولوت نباشند، آنگاه تغییر در فاصله محوری چرخ دنده ها باعث نقض قضیه اساسی چرخ دنده ها می شود و در نتیجه تغییرات در سرعت خروجی مشاهده خواهد شد.

اما اگر دندانه های چرخ دنده های درگیر اینولوت باشند، تغییر در فاصله محوری چرخ دنده ها، قضیه اساسی چرخ دنده ها را نقض نمی کند و تاثیری در برقراری نسبت ثابت بین سرعت های ورودی و خروجی ایجاد نمی کند. درواقع این اساسی ترین ویژگی دندانه های اینولوت می باشد که برای چرخ دنده ها درنظر گرفته می شود.

شکل زیر تاثیر تغییر فاصله محوری روی عملکرد چرخ دنده برای دندانه های اینولوت را نشان می دهد. مشاهده می شود که وجود اختلاف بین فاصله محورها، تنها زاویه فشار دندانه های درگیر را تغییر می دهد، اما همچنان محور های انتقال یا عمود مشترک ها از نقطه تماس دندانه ها عبور می کند که باعث می شوند نسبت سرعت ها ثابت بماند.

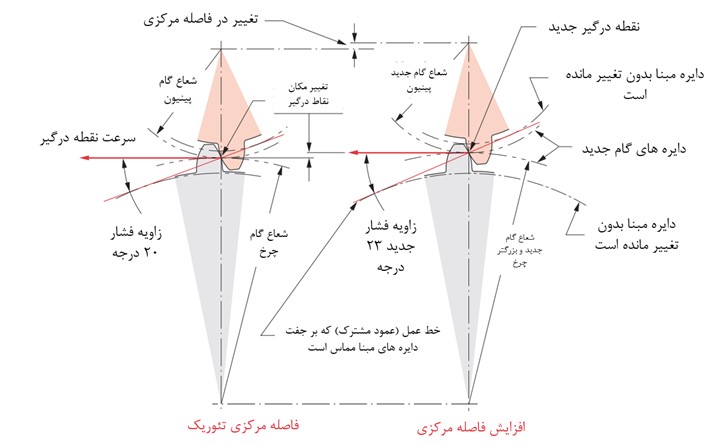
لقی و اثرات آن در چرخ دنده ها

لقی در درگیری دندانه ها که بر روی دایره گام اندازه گیری می شود مستقیما با تغییر فاصله محور های چرخ دنده ها زیاد یا کم می شود. اگر فاصله مرکزی را زیاد کنیم لقی زیاد می شود. لقی در چرخ دنده ها غیر قابل اجتناب است. بدین معنا که، ساخت چرخ دنده ای با لقی صفر امکان پذیر نیست. همچنین، در واقعیت نمی توان هندسه تمام دندانه ها را یکسان ساخت. لذا باید یک مقدار کمی درجه خلاصی بین صخامت دندانه (tooth thickness) و فاصله دندانه ها (face width) وجود داشته باشد. لازم به ذکر است که در مواقعی که چرخ دنده ها در یک جهت حرکت می کنند (ساعتگرد یا پادساعتگرد) یا به عبارت دیگر، تغییر جهت ندارند، مسئله لقی چندان اهمیتی برای طراحان ندارد چرا که در حین درگیری دندانه ها همیشه از یک طرف درگیر می شوند. اما با عوض شدن جهت دوران یا جهت گشتاور، دندانه ها جهت درگیری را عوض می کنند و اثر لقی با شنیدن صدای قابل توجهی مشاهده می شود. همچنین در این موارد، لقی باعث زیاد شدن خوردگی و سایش دندانه ها و تنش ها در آن ها می شود. انجمن چرخ دنده سازان آمریکا (AGMA) برای طراحی و ساخت چرخ دنده ها استاندارد های کیفی و تلرانس های مختلفی را در نظر گرفتند که از دقت پایین تا دقت بالا طبقه بندی می شوند که می توانید در ادرس https://members.agma.org/ مشاهده کنید. لازم به ذکر است که هزینه تهیه و ساخت چرخ دنده متناسب با استاندارد کیفی و دقت تلرانس های ساختی ارائه شده از سوی سازنده آن است.

نسبت درگیری (contact ratio)

هنگام انتقال قدرت بین دو چرخ دنده که از طریق درگیری دندانه ها صورت می گیرد، بررسی درگیری و ازاد شدن دندانه ها به شکل روان و به صورتی که درگیر شدن دندانه، قبل از ازاد شدن دندانه ی بعدی اتفاق بیوفتد، بسیار اهمیت دارد. لذا، یکی از پارامتر هایی که وضعیت درگیری دندانه هارا مشخص می کند نسبت درگیری می باشد. این نسبت برابر است با نسبت طول خط عمل با گام دایره مبنا.

این پارامتر نشان دهنده ی تعداد میانگین دندانه های درگیر حین انتقال قدرت است. این عدد اگر برابر یک باشد بدین معنی است که به محض ازاد شدن دندانه، دندانه بعدی درگیر می شود. این امر معمولا مطلوب نیست زیرا در این حالت اگر لقی بین دندانه ها وجود داشته باشد، اثرات ارتعاش در سرعت خروجی مشاهده می شود. همچنین در این حالت نیروی زیادی به سر دندانه وارد می شود که خمش حداکثری را به ریشه دندانه وارد میکند. هرچه این عدد بالاتر از یک باشد، نیروی تماس دو چرخ دنده بین دندانه ها تقسیم می شود. مقدار پیشنهادی حداقل این عدد برابر 1.2 است اما معمولا ترکیب چرخ دنده ها و مکانیزم های چرخ دنده ای این عدد تا 1.5 و بالاتر هم می باشد.

کاربرد سیستم های چرخ دنده ای

گیربکس های کاهنده

همانطور که به اهمیت مجموعه های چرخ دنده ای و اساس کارکرد این مکانیزم ها در ابتدای این مقاله اشاره شد، کاربرد این سیستم ها در صنایع مختلف، در وسایل و ماشین آلات مختلف بسیار وسیع خواهند بود. از جمله متداول ترین استفاده ی این مکانیزم های چرخ دنده ای در گیربکس های کاهنده است که خصوصا در صنایع سنگین کاربرد فراوان دارند. این گیربکس ها عموما با نسبت تبدیل ها و ظرفیت های مختلف یافت می شوند. در شکل زیر چند نمونه از گیربکس های کاهنده نشان داده می شود.

وظیفه اصلی گیربکس های کاهنده کاهش سرعت دورانی شفت ورودی و افزایش گشتاور شفت خروجی می باشد. گیربکس های کاهنده تعدادی چرخ دنده های درگیر در خود جای می دهد که نسبت ورودی به خروجی این چرخ دنده ها نسبت تبدیل گیربکس کاهنده می باشد. کاهش سرعت دورانی و افزایش گشتاور یکی از مواردی است که در ماشین آلات صنعتی برای بهبود عملکرد سیستم مورد استفاده قرار می گیرد. چرا که در اکثر مواقع، موتور های الکتریکی قادر به تولید گشتاور مورد نیاز انتقال ماشین آلات نیستند و گیربکس های کاهنده نقش مهمی را در بهبود عملکرد سیستم ها با القا کردن مزیت مکانیکی ایفا می کند. معمولا ابتدای گیربکس کاهنده (یا شفت ورودی) یک چرخ دنده با شعاع دایره مبنای کوچکتر و در خروجی گیربکس، یک چرخ دنده با قطر دایره مبنای بزرگتر قرار می گیرد. شکل زیر شمای کلی یک گیربکس کاهنده را نشان می دهد که دارای سه محور می باشد. به طور کلی درمجموعه های چرخ دنده ای که دارای چند محور (یا شفت) هستند و حداقل دو چرخ دنده روی آن ها سوار هستند، مجموعه های چرخ دنده ای مرکب گفته می شود.

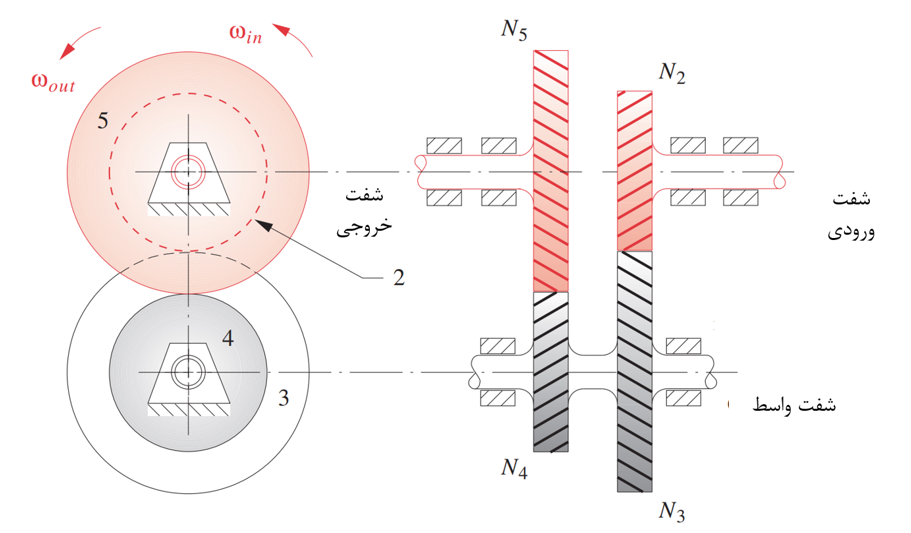
یکی از مکانیزم های چرخ دنده ای مورد استفاده در گیربکس های کاهنده، مجموعه سه محوری مطابق شکل زیر است که دارای شفت ورودی، شفت خروجی، شفت واسط یا Idler که انتقال قدرت را از شفت ورودی به شفت خروجی منتقل می کند و جهت دوران را حفظ می کند. در این مکانیزم، چرخ دنده ها با تعداد دندانه های مختلفی می توانند قرار گیرند و نسبت تبدیل متفاوتی را ایجاد کنند. به طور یک قاعده نسبت تبدیل مجموعه های چرخ دنده ای مرکب به صورت نسبت حاصل ضرب تعداد دندانه های چرخ دنده های راننده (driver) به حاصل ضرب تعداد دندانه های چرخ دنده های رونده (driven) می باشد. به عنوان مثال در شکل زیر:

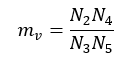
توجه داشته باشیم که در مجموعه مرکب زیر، چرخ دنده 2 چرخ دنده 3 را به حرکت در می آورد. پس 2 = راننده، 3 = رونده. به دلیل اینکه چرخ دنده 3 که بر روی شفت واسط قرار دارد به حرکت در آمده است، شفت واسط نیز شروع به دوران می کند و چرخ دنده 4 نیز همراه با آن حرکت می کند. لذا در جفت چرخ دنده ای 4 و 5، چرخ دنده شماره 4 راننده و شماره 5 رونده می شوند.

گیربکس های کاهنده می توانند انواع مختلفی داشته باشند از جمله ی آن ها، گیربکس های کاهنده راست گرد هستند که شفت خروجی زاویه 90 درجه ساعتگرد با شفت ورودی دارد. شکل زیر چند نمونه متداول این گیربکس ها را نشان می دهد. دراین گیربکس ها از چرخ دنده های حلزونی به طور متداول استفاده می شود که زاویه شفت ورودی را 90 درجه با شفت دیگر انحراف دهد. همچنین گیربکس های کاهنده راست گرد می توانند چند مرحله ای یا دارای چند شفت باشند (مثلا 4 شفت) مانند عکس بالا. سازندگان مختلفی گیربکس های کاهنده راست گرد را تولید میکنند از جمله :

https://www.winsmith.com/

https://www.evergeardriving.com

https://www.reckondrives.com

گیربکس های خورشیدی

همانگونه که مطرح شد، گیربکس های کاهنده در انواع مختلف و با نسبت تبدیل های مختلف می توانند تعداد شفت های مختلفی داشته باشند. عمدتا در این گیربکس ها به دلیل ساده بودن مکانیزم های چرخ دنده ای آن ها چندین شفت (گاه زوایای مختلف نسبت به هم) استفاده می شود و انتقال قدرت از شفت ورودی به شفت خروجی به طور مستقیم یا به واسطه شفت های واسط دیگر صورت می پذیرد. اما یکی از ضعف های این گیربکس ها فضای زیاد و وزن زیادی هست که به واسطه داشتن چند محور و یاتاقان ها، اب بندی ها و غیره دارد. گیربکس های خورشیدی یا اپی سیکلیک این ضعف را پوشش داده اند به طوریکه در این گیربکس ها شفت ورودی با شفت خروجی هم مرکز هستند و محورهای مختلف با زوایای مختلف در این گیربکس ها وجود ندارد. به بیان دیگر، گیربکس های خورشیدی از جمله گیربکس های با راندمان بالا و متراکم از نظر فضای اشغالی در صنعت به کار گرفته می شوند. اما مکانیزم چرخ دنده ای به کار رفته در این گیربکس ها دارای پیچیدگی مکانیکی و طراحی و تحلیل آن ها کار دشواری است. شکل زیر چند نمونه از این گیربکس هارا نشان می دهد.

صنایعی که در آن ها دقت، کنترل پذیری، محدودیت فضا، راندمان در انتقال قدرت مهم می باشند از گیربکس های خورشیدی استفاده می کنند. از جمله این صنایع می توان به صنایع رباتیک، خودرو، توربین، هوافضا، پزشکی اشاره کرد. اما ساختن این گونه گیربکس ها چالش های ساختی فراوانی را به دنبال دارد چرا که به دلیل فضای کم اشغالی و ظرفیت بالای گشتاور، گرمای زیادی تولید می کنند. درواقع به دلیل پیچیدگی مکانیکی و مکانیزمی این گیربکس ها که چرخ دنده های زیادی باهم درگیر هستند که این تماس های زیاد بین چرخ دنده ها حرارت زیادی تولید می کنند. همچنین تعمیر و نگهداری این گیربکس ها با چالش هایی نیز مواجه است.

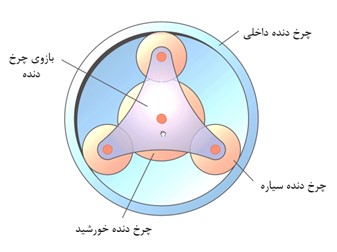
به طور کلی این مجموعه های چرخ دنده ای از 4 بخش چرخ دندنه داخلی، چرخ دنده خورشید، چرخ دنده های سیاره ای و یک بازو carrier که چرخ دنده های سیاره رو به هم متصل میکند و با چرخ دنده خورشید هم مرکز می باشد. اجزای اصلی در شکل زیر نشان داده شده اند. شفت ورودی می تواند به چرخ دنده خورشید متصل باشد و شفت خروجی به بازو carrier. درواقع با دوران چرخ دنده خورشید، مجموعه چرخ دنده های سیاره ای که از یک طرف با چرخ دنده خورشید و از طرف دیگر با چرخ دنده داخلی فیکس درگیر هستند، شروع به چرخش حول محور گیربکس می کنند و در نتیجه بازوی carrier نیز حلو این محور دوران می کند و با نسبتی مشخص سرعت و گشتاور را انتقال می دهد. لازم به ذکر است که این گونه گیربکس ها می توانند دارای چند استیج یا چند مجموعه خورشیدی باشند و نسبت های تبدیل مختلفی را داشته باشند. که در شکل زیر نشان داده شده اند.